Kaggle z SAS - część druga
- 4 września 2017
- Autor: Piotr Florczyk
- Category: Publikacje

W poprzedniej części cyklu, “Kaggle z SAS-pierwsze kroki z danymi” przy pomocy SAS University Edition (dalej SAS UE) eksplorowaliśmy dane aby zapoznać się z ich podstawowymi charakterystykami. Tym razem zajmiemy się wstępnym przygotowaniem danych oraz zbudujemy prosty model klasyfikujący za pomocą regresji logistycznej.
Zanim przystąpimy do modelowania powinniśmy dane podzielić na dwie części tj. trenującą i walidacyjną. Jest to typowy zabieg stosowany w celu uniknięcia tzw. „przetrenowania modelu” oraz ułatwienia oceny jego jakości. W przypadku budowy wielu modeli zbiór walidacyjny może posłużyć do wyboru najlepszego z nich. Zazwyczaj stosuje się podziały 50/50 (50% na część trenującą i 50% na walidacyjna), 60/40, 70/30 czy też 80/20. Zależy to od preferencji modelarza oraz ilości danych jakimi dysponujemy. Podział nie może być przypadkowy. Musimy mieć pewność, że obie części mają równe proporcje zmiennej, którą będziemy modelować dlatego należy zastosować losowanie warstwowe (stratified sampling). W tym celu użyjemy procedury surveyselect dostępnej w SAS UE. Procedura wymaga aby zbiór danych był posortowany po zmiennej identyfikującej warstwy (stratifying variable). W celu weryfikacji poprawnego podziału danych warto wygenerować tabelę częstości.
proc sort data=train out=train_sorted; by Survived;run;proc surveyselect data=train_sorted out=train_survey outall samprate=0.7 seed=12345; strata Survived;run;proc freq data=train_survey; tables Selected*Survived;run;
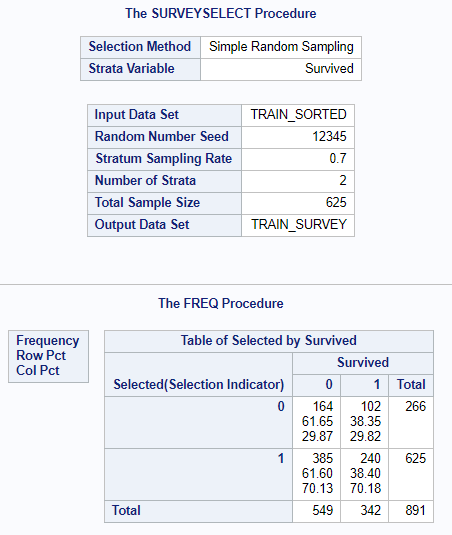
Zmienna Selected o wartości 1 będzie oznaczała obserwację z części trenującej. Zróbmy jeszcze szybką obróbkę zbioru aby pozostawić tylko interesujące nas kolumny i odpowiednio nazwać zmienne.
data titanic; set train_survey; rename Selected=Part; drop SelectionProb SamplingWeight;run;
Do modelowania zmiennej binarnej (jaką jest zmienna Survived) doskonale nadają się regresja logistyczna. Aby zbudować model oraz go użyć musimy być pewni, że każda obserwacja ma komplet danych tj. wszystkie kolumny dla danej obserwacji mają przypisane wartości. Przypomnijmy ile mamy braków danych w poszczególnych zmiennych (dane z poprzedniego artykułu naszego cyklu):
| Zmienna | Liczba braków danych |
| Age | 177 (19.87%) |
| Embarked | 2 (0.22%) |
| Fare | 0 (0.00%) |
| Parch | 0 (0.00%) |
| Pclass | 0 (0.00%) |
| Sex | 0 (0.00%) |
| SibSp | 0 (0.00%) |
Zmienna Age ma aż 177 braków danych. Stanowi to prawie 20% zbioru. Gdybyśmy rozpoczęli modelowanie na nieuzupełnionych danych, algorytm odrzuciłby te 20% obserwacji. Stracilibyśmy w ten sposób bardzo dużą część informacji zawartych w zbiorze. Pośród zmiennych klasyfikujących braki danych zaktualizowaliśmy w zmiennych Embarked. W poprzednim artykule zdecydowaliśmy, że zmienną Cabin pominiemy i nie będziemy używać w modelowaniu z powodu zbyt dużej liczby poziomów oraz ogromnej proporcji braków danych (ok. 77%). Wrócimy jeszcze do niej w kolejnej części artykułu.
Dla zmiennych ciągłych braki danych zastąpimy średnimi a dla zmiennych kategorycznych, medianą. Wartości imputowane powinny być wyliczone na części trenującej a następnie użyte do uzupełnienia zarówno części trenującej jak i walidacyjnej. Mimo, że w niektórych zmiennych nie pojawiają się braki danych to warty by zabezpieczyć się na taką ewentualność. Dlatego kod przygotujemy tak aby uwzględniał również te zmienne.
title "Średnia dla zmiennej Age i Fare w zbiorze trenującym";proc means data=titanic mean; where part=1; var Age Fare;run;
title "Tabele częstości dla zmiennych kategoryzujących w zbiorze trenującym";proc freq data=titanic order=freq; where part=1; tables Embarked; tables Parch; tables Pclass; tables SibSp; tables Sex;run;
Powyższe kody wskażą nam wartości do imputacji braków danych.
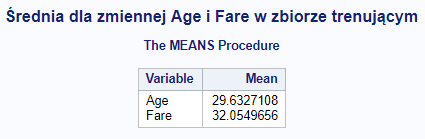
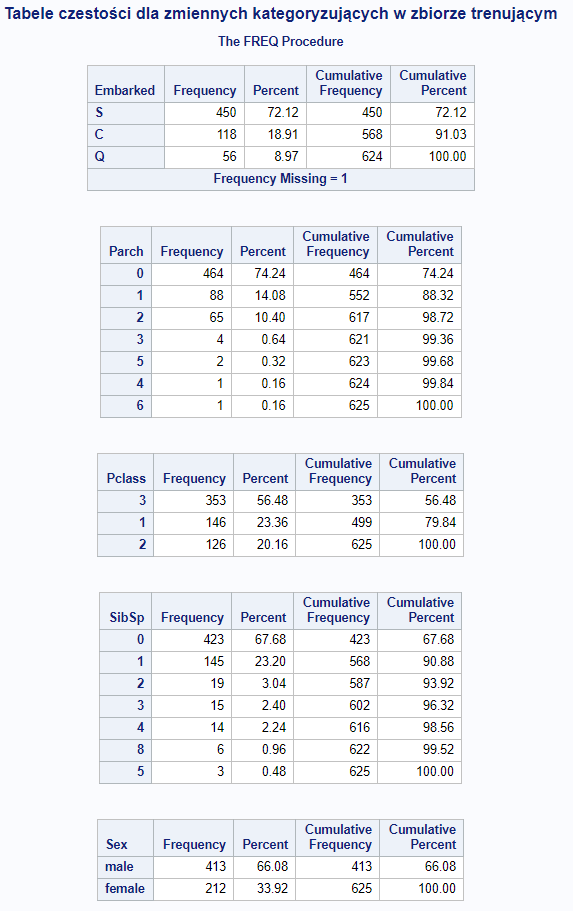
Zatem wykonajmy imputację
data titanic; set titanic; if Age = . then Age = 29.63; if Embarked = ' ' then Embarked = 'S'; if Fare = . then Fare = 32.05; if Parch = . then Parch = 0; if Pclass = . then Pclass = 3; if Sex = ' ' then Sex = 'male'; if SibSp = . then SibSp = 0;run;
Teraz możemy przystąpić do modelowania. W tym celu wykorzystamy procedurę logistic na danych trenujących. Wygenerowany model zapiszemy, a następnie użyjemy go aby wykonać scoring wszystkich obserwacji. Następnie sprawdzimy w ilu przypadkach nasz model się mylił a w ilu miał rację w podziale na dane trenujące i walidacyjne.
proc logistic data=titanic; where part=1; class Embarked Parch Pclass Sex SibSp Survived; model Survived(event='1') = Age Fare Embarked Parch Pclass Sex SibSp / selection=stepwise expb; store titanic_logistic;run;proc plm source=titanic_logistic; score data=titanic out=titanic_scored predicted=p / ilink;run;data titanic_model_score; set titanic_scored; if Survived = 1 and p > 0.5 then good = 1; else if Survived = 0 and p <= 0.5 then good = 1; else good = 0;run;proc freq data=titanic_model_score; tables part*good / nocol nopercent;run;
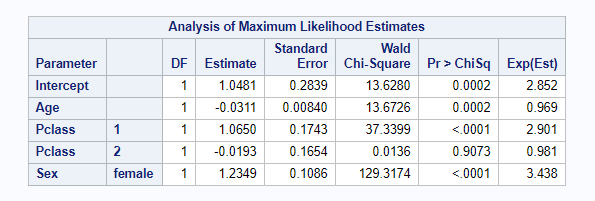
Algorytm dobierania zmiennych zdecydował, że w modelu będą zmienne Age, Pclass oraz Sex.
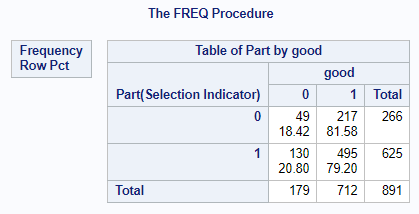
Zarówno dla zbioru trenującego (Part=1) jak i walidacyjnego (Part = 0), proporcja poprawnie zaklasyfikowanych przypadków (good=1) jest zbliżona. Wynosi 79.20% i 81.58% dla odpowiednio dla zbioru trenującego i walidacyjnego. Przez to widzimy, że bez większego nakładu pracy otrzymaliśmy model zachowujący się stabilnie z całekim przyzwoitym wynikiem.
Zobaczmy jak wypadamy w konkursie. W celu wysłania naszego wyniku potrzebujemy zrobić scoring danych zbioru test.csv i wysłać wynik na stronę Kaggle.
proc import file="/folders/myfolders/test.csv" out=test replace;run;
data test; set test; if Age = . then Age = 29.63; if Embarked = ' ' then Embarked = 'S'; if Fare = . then Fare = 32.05; if Parch = . then Parch = 0; if Pclass = . then Pclass = 3; if Sex = ' ' then Sex = 'male'; if SibSp = . then SibSp = 0;run;proc plm source=titanic_logistic; score data=test out=test_scored predicted=p / ilink;run;data test_scored; set test_scored; if p > 0.5 then Survived = 1; else Survived = 0; keep PassengerId Survived;run;proc export data=test_scored file="/folders/myfolders/simple_logistic.csv" replace;run;
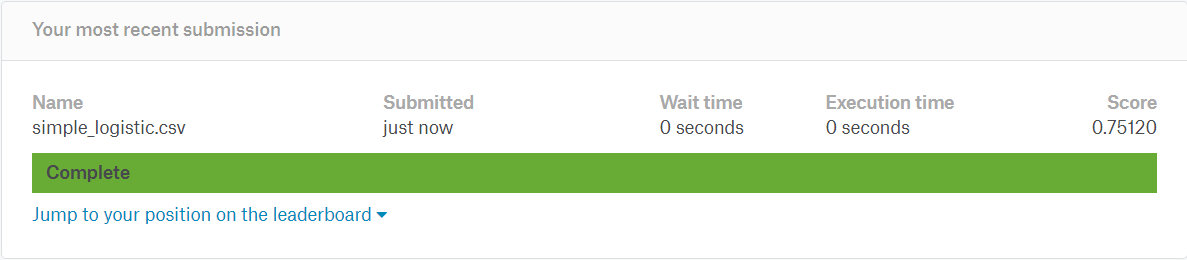
Biorąc pod uwagę fakt, że do modelu używamy tylko trzech zmiennych, wynik 75.12% nie jest zły. Mamy do dyspozycji jeszcze kilka kolumn więc stać nas na więcej. Naszym celem jest minimum 80%. Co możemy zrobić aby poprawić ten wynik?
- W imionach możemy znaleźć tytuł danej osoby tj. Mr, Mrs, Miss, Don, Sir itp.
- Może to głupie ale spróbujmy wyliczyć długość nazwiska.
- Numery biletów powtarzają się poszczególnych obserwacjach. Prawdopodobnie są bilety rodzinne i pojedyncze.
- Poszukajmy w internecie planów Titanica. Może na podstawie numerów kajut możemy wskazać gdzie dana kajuta się znajdowała. Pokład, lewa/prawa burta, rufa itp.
Jak widać jest jeszcze sporo pomysłów, które warto zweryfikować bo może się okazać, że damy radę wyciągnąć z danych o wiele więcej informacji niż nam się początkowo wydawało. To wszystko w następnej części.

AUTOR
Piotr Florczyk
Absolwent Wydziału Elektroniki i Technik Informacyjnych Politechniki Warszawskiej na kierunku Elektronika, Informatyki i Telekomunikacja. Ponad pięć lat pracował w SAS Institute Polska gdzie rozwijał umiejętności trenerskie oraz zdobywał wiedzę i doświadczenie uczestnicząc w projektach. Trener szkoleniowiec i prezenter na wielu konferencjach organizowanych przez SAS. Specjalizuje się w analityce biznesowej oraz przetwarzaniu dużych wolumenów danych na systemach rozproszonych.
