Założona w 2010 roku przez Anthonego Goldbluma platforma dla konkursów analitycznych oraz modelowania predykcyjnego Kaggle jest obecnie znana prawie każdemu kto miał styczność z dziedziną zwaną Data Science. Dzięki bogatej bazie zbiorów danych, prostocie obsługi oraz w głównej mierze społeczności, przez lata zyskała olbrzymią popularność.

Istnieje wiele poradników pomagających otworzyć drzwi do rozbudzającego wyobraźnię świata  eksploracji i modelowania danych. Większość z tych poradników bazuje na bardzo przystępnych do zrozumienia danych z informacjami o pasażerach Titanica.  Naszym celem jest jak najdokładniej określić szanse przeżycia danej osoby na podstawie jej płci, wieku, klasy podróży czy miejsca rozpoczęcia wyprawy. W przykładach wykorzystane są dostępne powszechnie narzędzia oraz pakiety przeznaczone do modelowania tj. R, Python czy nawet wszystkim znany Microsoft Excel. Ku mojemu zdziwieniu, nigdzie nie znalazłem kompletnego przykładu z wykorzystaniem jednego z najlepszych narzędzi do zaawansowanej analityki na rynku, jakim jest SAS. Mogą tu się podnieść głosy typu “SAS nie jest darmowy” czy “nie każdy ma dostęp do oprogramowania SAS”. Otóż nic bardziej mylnego! Od kilku już lat istnieje darmowa, edukacyjna wersja tego oprogramowania pod nazwą SAS University Edition. Zawiera w sobie wszystkie niezbędne komponenty aby rozpocząć pracę z danymi i ich modelowaniem. Najnowsza wersja 3.6 jest wzbogacona o Jupyter Notebook, ułatwiający porządkowanie kodu, opisów i analiz.

Celem tutorialu jest zaprezentowanie jak wykorzystać możliwości SAS University Edition do nauki modelowania. Nie chcę tutaj poruszać całej metodyki przygotowania do modelowania i samego modelowania danych. Ta dziedzina jest tak obszerna, że te kilka artykułów rozrosłoby się do rozmiarów książki. Nadal, tutorial jaki przygotowałem stał się zbyt długi jak na jeden wpis, dlatego musiałem rozbić go na kilka części.

Część pierwsza tutorialu będzie dotyczyła zapoznania się z danymi oraz podstawowej analizy. Dzięki wglądowi w dane będziemy mogli wyciągnąć wstępne wnioski i zaplanować dalsze kroki.

W następnym wpisie zajmiemy się budową modelu regresji logistycznej i ocenimy jego stopień dopasowania. Wyślemy również pierwsze wyniki modelowania do Kaggle i zastanowimy się co możemy zrobić aby poprawić wynik punktowy przyznany przez Kaggle. Trzecia część będzie implementacją rozważań z drugiego wpisu. Skupimy się na inżynierii oraz ekstrakcji cech i sprawdzimy czy nasza dodatkowa praca przyniesie wymierne rezultaty.

W tych trzech wpisach skupimy się raczej na tym jak wykonać analizy w SAS UE oraz zinterpretować wyniki ale bez zagłębiania się w składnię języka SAS. Zainteresowanych odsyłam do dwóch świetnie przygotowanych darmowych szkoleń z podstaw języka SAS oraz z podstaw modelowania danych w SAS. Dają solidne fundamenty do pracy z tym językiem.

• https://support.sas.com/edu/schedules.html?id=2588&ctry=PL
• https://support.sas.com/edu/schedules.html?id=2816&ctry=PL

Ostania część nie będzie bezpośrednio kontynuacją tutorialu ale będzie ściśle z nim związana. Przedstawię narzędzie z najwyższej półki przeznaczone do modelowania ze stajni SAS czyli SAS Enterprise Miner i w nim wykonamy wszystkie dotychczasowe analizy i modelowania. Nie będzie to nauka obsługi tego narzędzia ale raczej wypunktowanie przewag jakie daje ten interfejs w porównaniu z pisaniem samych kodów.

Pierwszym krokiem po zainstalowaniu i uruchomieniu SAS University Edition będzie pobranie danych i zaimportowanie ich do SAS. Skorzystamy tutaj z wspomnianego wcześniej zbioru Titanic, który można znaleźć na stronie Kaggle. (https://www.kaggle.com/c/titanic/data). Pobieramy plik train.csv, którego użyjemy do modelowania. Drugi plik, test.csv, będzie potrzebny później. Zbiory należy załadować do SAS Studio, przeglądarkowego interfejsu programisty SAS.

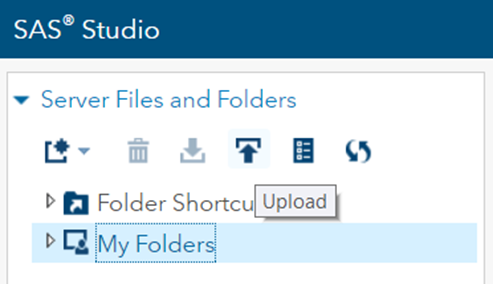
Załadowane dane należy przekonwertować do natywnego formatu SAS. W tym celu w oknie programu piszemy poniższy kod. Program uruchamiamy całościowo klawiszem F3, bądź fragmentami wcześniej zaznaczając interesujące nas linie i wciskając klawisz F3.

proc import file='/folders/myfolders/train.csv' out=train replace;
run;

W SAS-ie wyróżnia się dwa typy danych: numeryczny i znakowy. Podczas importu SAS automatycznie rozpoznaje i przypisuje typy danych odpowiednim zmiennym.

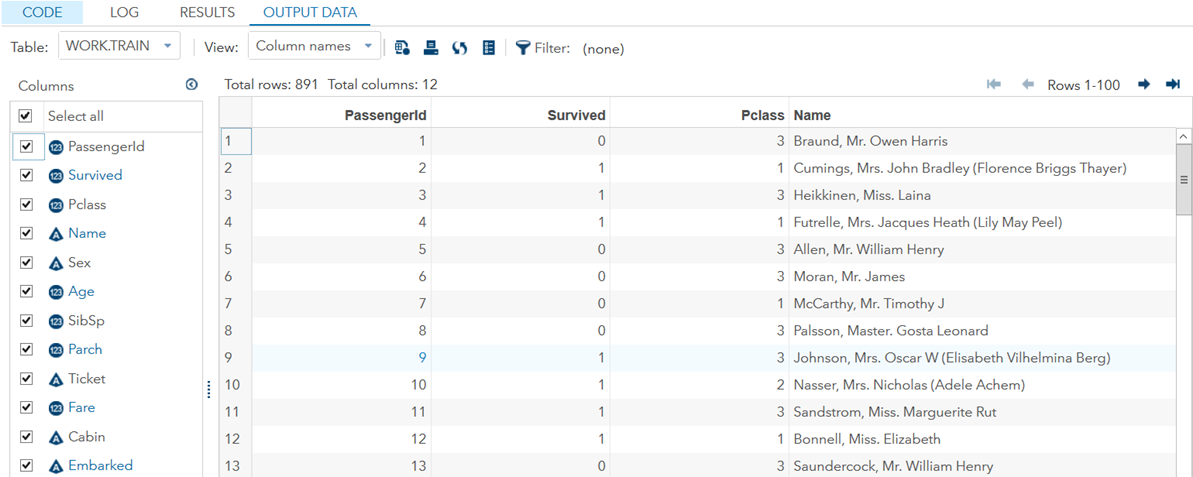
Zanim przystąpimy do modelowania należy zapoznać się z danymi tj. Określić użyteczność zmiennych, wyliczyć podstawowe statystyki, wykreślić rozkłady, sprawdzić liczbę unikalnych wartości dla zmiennych oraz zależność ze zmienną zależną. Tą zmienną jest Survived z informacją czy pasażer przeżył (1) czy nie (0). Zmienna PassengerId jest tylko identyfikatorem pasażera i nie będzie brana pod uwagę przy modelowaniu. Podobnie jak Name oraz Ticket. Za pomocą prostych operacji dałoby się wyciągnąć z tych zmiennych dodatkowe cechy, które mogłyby się okazać użyteczne. O ekstrakcji cech innym razem. Opis pozostałych zmiennych jest dostępny na stronie konkursu Kaggle i lepiej się z nim zapoznać. Tu od razu przechodzimy do obliczeń.

title "Podstawowe statystyki dla wszystkich zmiennych numerycznych";
proc means data=train nmiss mean std median min max;
run;

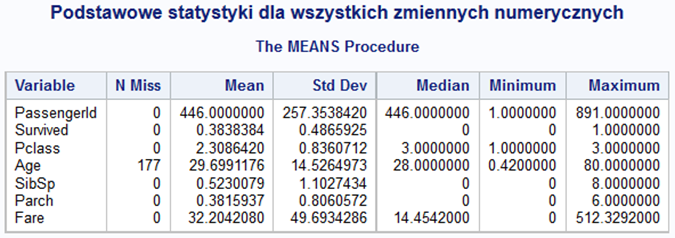
Na pewno będziemy musieli uporać się z brakami danych w kolumnie zmiennej Age. Zmienne Pclass (klasa podróży), SibSp (liczba rodzeństwa + partner podróżujących razem) i Parch (liczba dzieci bądź rodziców podróżujących razem) nie mają tego problemu. Natomiast, sądząc po opisie zmiennych oraz zakresie, lepszym podejściem będzie potraktowanie ich jako zmienne kategoryzujące. Zobaczmy więc, jaki jest rozkład poziomów tych zmiennych oraz dla zmiennej Survived i zmiennych tekstowych.

title "Tabele częstości dla niektórych zmiennych";
proc freq data=train nlevels;
tables Survived;
tables Sex;
tables Pclass;
tables SibSp;
tables Parch;
tables Embarked;
tables Cabin;
run;

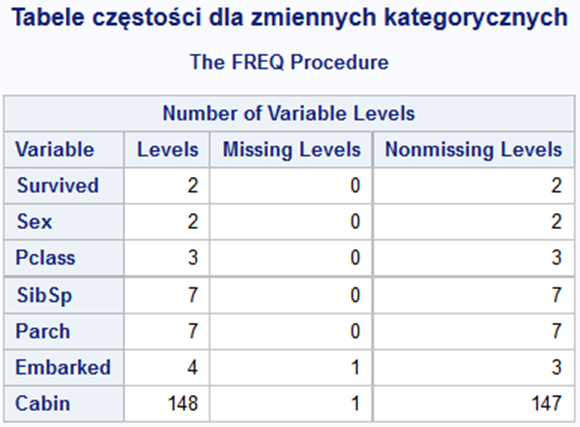
(fragment rezultatów)

Liczba poziomów zmiennej Cabin jest zbyt duża. W standardowym przypadku należałoby tę liczbę zredukować. Spójrzmy na tabelę z częstościami

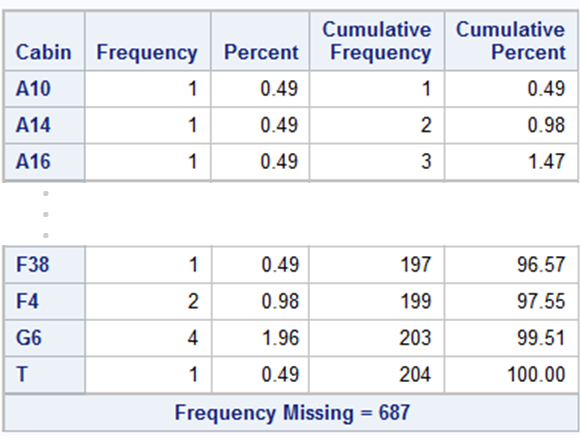
Liczba braków wartości (687 czyli ok. 77%) dla tej zmiennej eliminuje ją z listy zmiennych do modelowania. Dodatkowo, czy numer kajuty pasażera będzie dobrym predyktorem tego czy ktoś przeżyje katastrofę czy nie? Być może sama litera przed numerem wniesie dodatkową wartość do modelowania. Nad tą zmienną można się dokładniej pochylić w kolejnym podejściu do rozwiązania problemu.. Ale tym razem zostanie pominięta.W rezultatach możemy obejrzeć jakie są proporcje poszczególnych poziomów zmiennych. Tabelki nie są najłatwiejszą formą interpretacji wartości dlatego użyjmy wykresów. Kod do wygenerowania jedngoo z nich zamieszczony jest poniżej.

title "Rozkład lokalizacji zaokrętowania";
proc sgplot data=train;
vbar Embarked / datalabel missing;
label Embarked = "Passenger Embarking Port";
run;

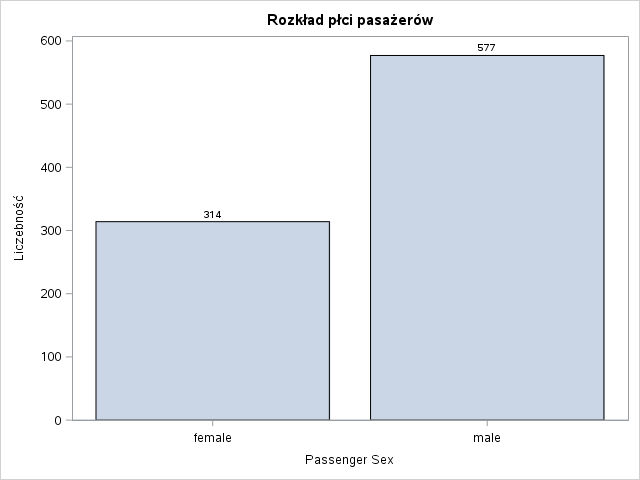
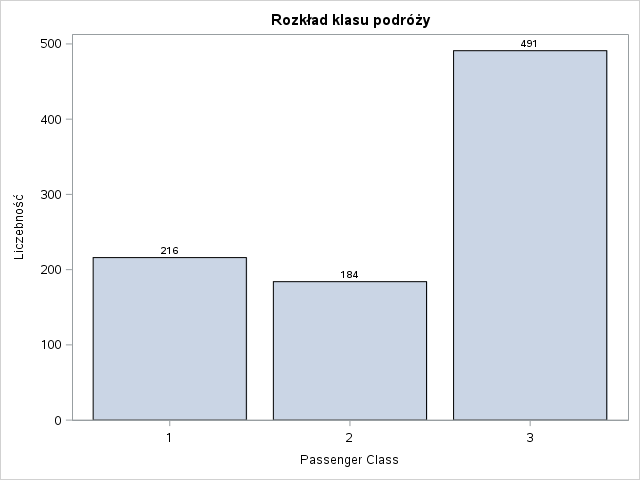
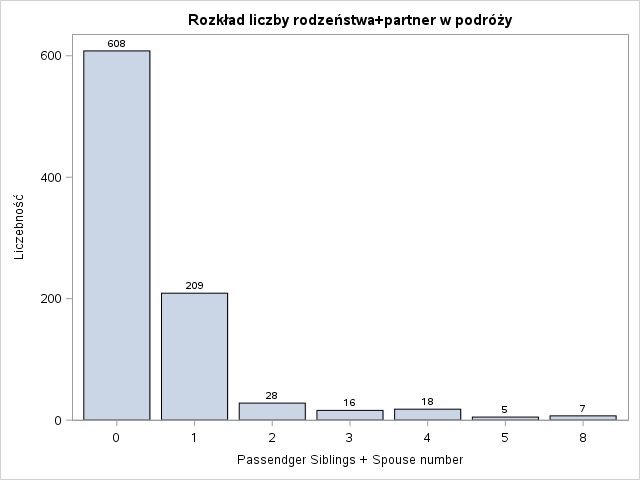
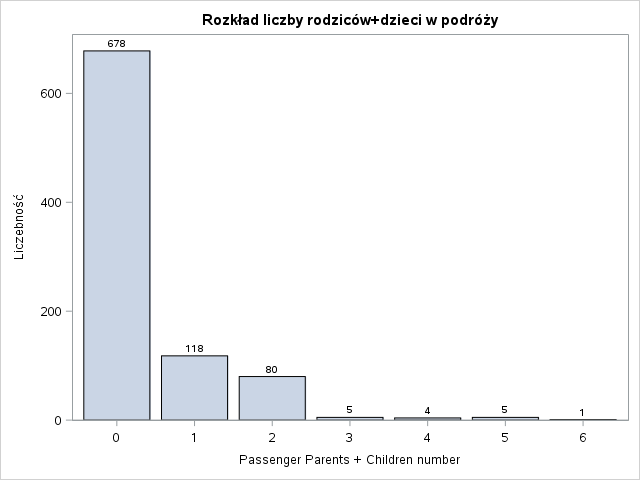
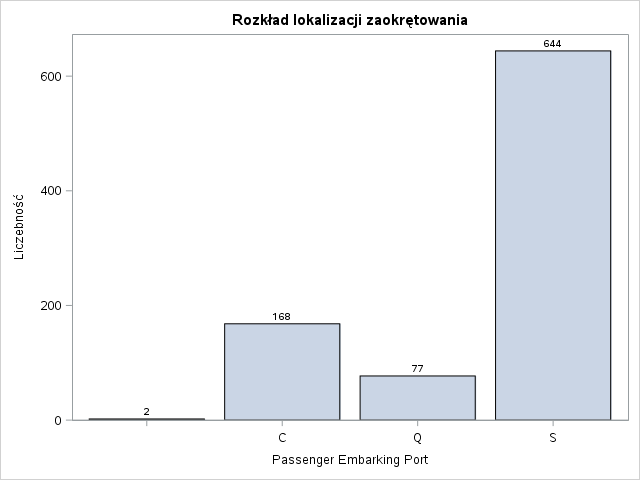
W rozkładach wartości nie widać nic nadzwyczajnego. Dla portu zaokrętowania mamy dwa brakujące wartości. Uzupełnimy je modą (S). Przyjrzyjmy się teraz jakie są proporcje przeżycia w poszczególnych poziomach tych zmiennych.

title "Embarked vs Survived";
proc sgplot data=train pctlevel=group;
vbar Embarked / group=Survived stat=percent missing;
label Embarked = "Passenger Embarking Port";
run;

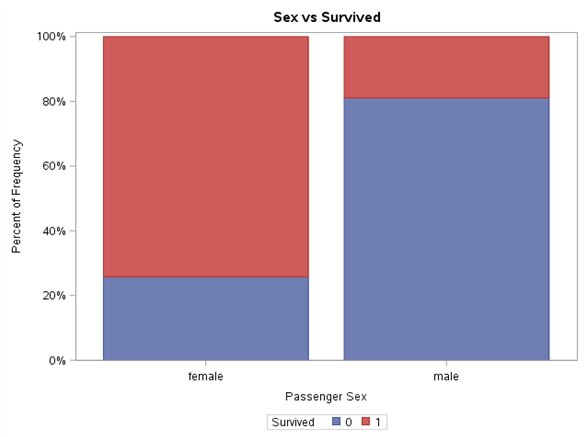
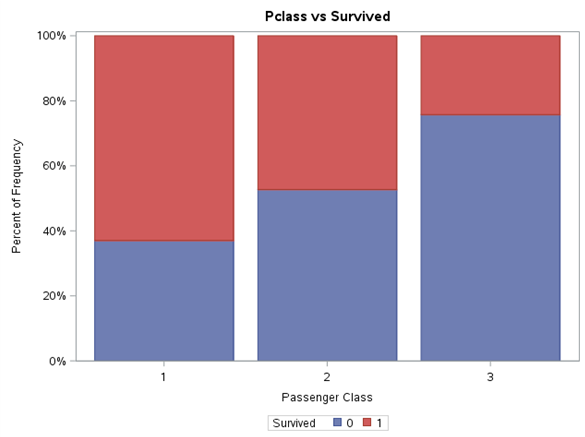
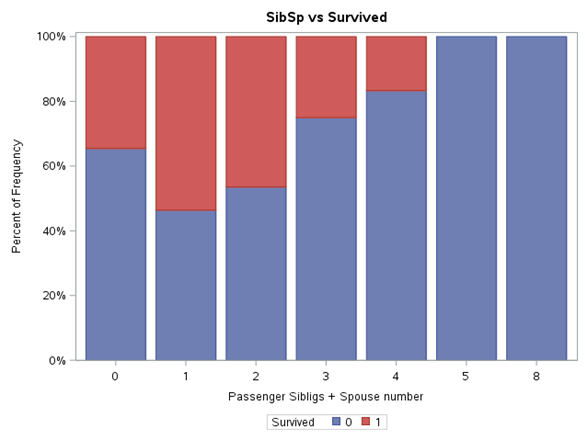
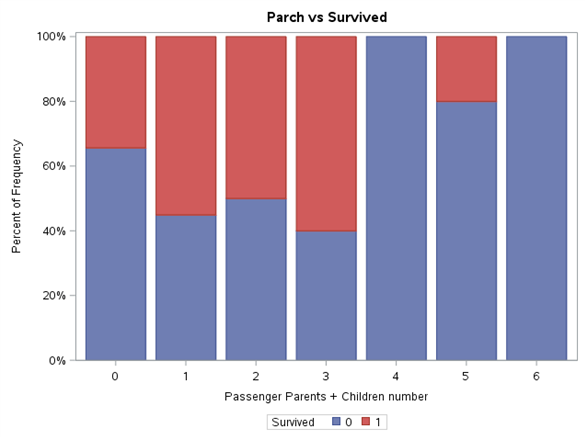
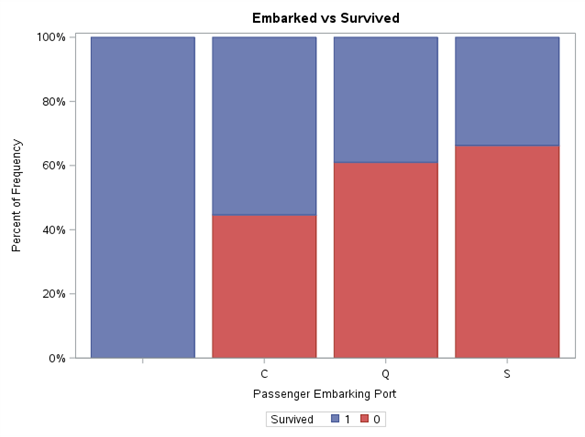
Każdy z poziomów zmiennej został znormalizowany do przedziału 0%-100%. Dzięki takiej prezentacji wyników łatwiej jest zaobserwować różnice w proporcji wartości zmiennej Survived pomiędzy poziomami tej samej zmiennej oraz wyciągnąć wstępne wnioski. Na pewno bardzo wysoki wpływ na przeżywalność ma płeć. W myśl zasady “kobiety i dzieci pierwsze”, można się spodziewać, że wiek również będzie grał ważną rolę w modelu. Klasa podróży również pokazuje tendencję większej przeżywalności wraz z jej wzrostem. Dla zmiennej SibSp można się zastanowić czy nie wrzucić wartości większych od 4 w jeden worek. Są to mało liczne poziomy oraz zmienna Survived dla nich przyjmuje wartości 0. Podobne podejście można zastosować dla zmiennej Parch.

Dla zmiennych ciągłych przeprowadźmy podobną analizę.

title "Rozkład wartości wieku";
proc sgplot data=train;
histogram Age / binwidth=1;
run;
title "Age vs Survived";
proc sgplot data=train;
histogram Age / binwidth=1 group=Survived fillattrs=(transparency=0.5 );
run;

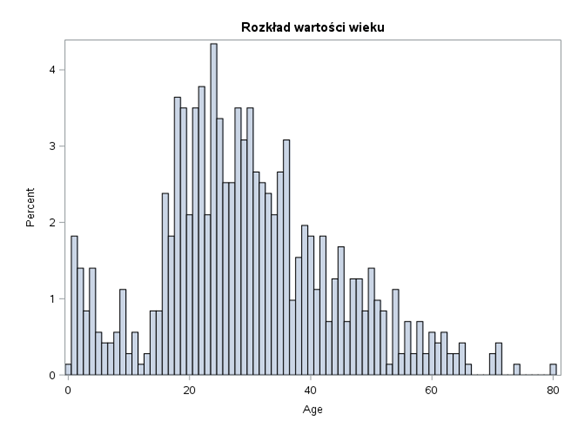
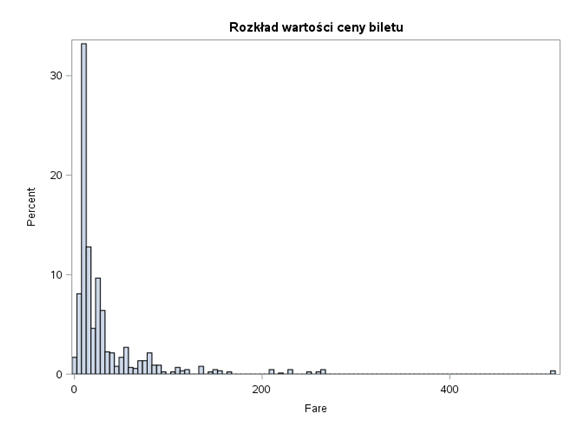
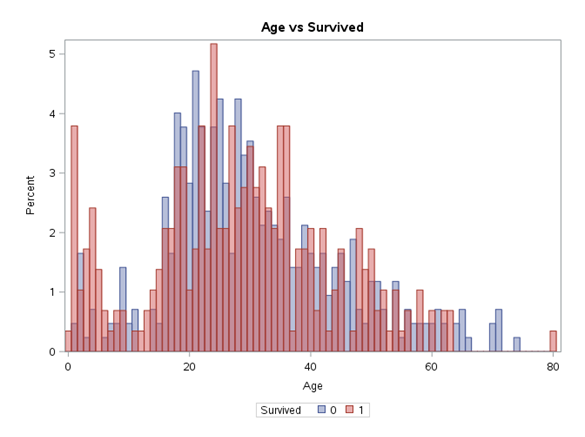
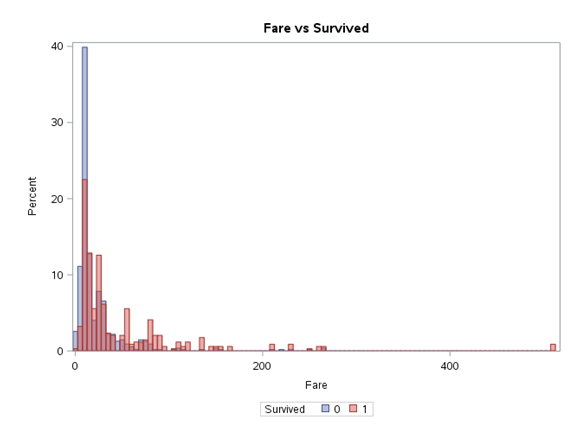
Można przypuszczać, że zmienna Fare jest skorelowana ze zmienną Pclass. Wyższa klasa podróży to wyższa cena biletu. Możemy odrzucić jedną z nich albo pozwolić algorytmowi modelowania na zdecydowanie, która będzie lepsza. Przy zmiennej Age widać, że w przedziale do ok. 15 lat, czyli dzieci, przeżywalność jest większa. Następnie spada a na koniec znowu delikatnie wzrasta. Ten wzrost pod koniec może być również związany ze statusem socjoekonomicznym.

Po przeprowadzeniu takiej wstępnej analizy wiemy już jakich danych możemy się spodziewać oraz jesteśmy w stanie zaplanować kolejne kroki, które przygotują je do modelowania. W kolejnym wpisie zajmiemy się uzupełnieniem braków danych oraz zbudujemy prosty model, który przetestujemy za pomocą danych z pliku test.csv.